• 1. Computer Graphics
  • 1.1. Screen
  • 1.2. Colours
  • 1.3. Rasterisation
  • 1.4. Anti-Aliasing
  • 1.5. Geometric Transformations
  • 1.6. Curves
    • 1.6.1. Bézier Curve
    • 1.6.2. Quadratic and Cubic Bézier Curves
    • 1.6.3. De Casteljau Algorithm
    • 1.6.4. Unit-Summary
  • 1.7. Paths
  • 1.8. Self Assessment
  • 1.9. Summary
  • 1.10. Recommended Reading
  • 1.11. Glossary
  • 1.12. Bibliography
  • 1.13. Metadata

1.6.2. Quadratic and Cubic Bézier Curves

Quadratic Bézier Curve

A quadratic Bézier curve is a Bézier curve of degree 2 and is defined through 3 points (P₀, P₁ and P₂)

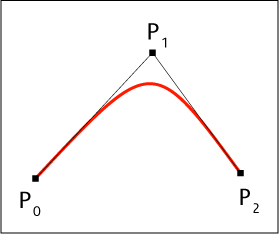Quadratic Bézier curve

Cubic Bézier Curve

A cubic Bézier curve is a Bézier curve of degree 3 and is defined by 4 points (P₀, P₁, P₂ and P₃). The curve starts at P₀ and stops at P₃. The line P₀P₁ is the tangent of the curve in point P₀. And so it is the line P₂P₃ in point P₃. In general, the curve will not pass through P₁ or P₂; the only function of these points is providing directional information. The distance between P₀ and P₁ determines “how long” the curve moves into direction P₁ before turning towards P₃.

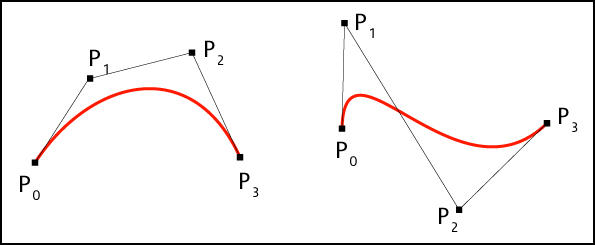Cubic Bézier curve

Now by considering the applied knowledge about Bézier curves, experience the Cubic Bézier Curve in the following interaction part a second time by moving the blue circles.

Update: 26.1.2012 (eLML) - Contact - Print (PDF) - © CartouCHe 2004-2007 (Creative Commons) - layout based on YAML