1.6.1. Bézier Curve

Formula of Bézier Curves

Bézier curves are widely used in computer graphics to model smooth curves.

A n-dimensional Bèzier curve is a curve of degree n. It is composed of Bernstein basis polynomials of degree n: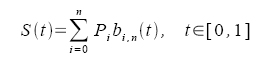



with the Bernstein basis polynomials of degree n defined as: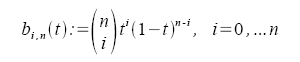

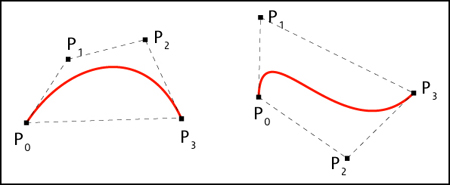
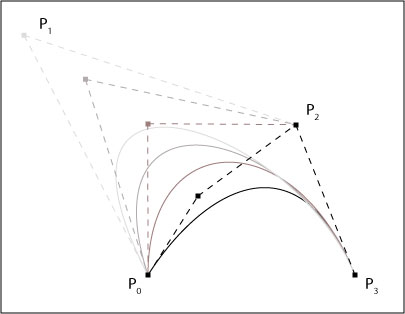
P_i is called control point for the Bézier curve. By connecting all control points with lines, we receive a polygon - starting in P₀ and finishing in P_n - that is called Bézier polygon. The Bézier curve is completely contained in the hull built from the Bézier polygon.

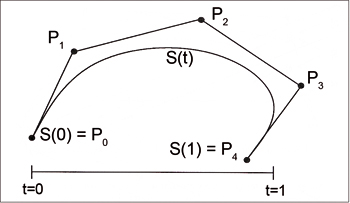Bézier Curve of degree 4. (GIGER-HOFMANN 1992)

We go back to the issue of the Berstein polynomials: The Bernstein polynomials are the weighting functions for Bézier curves. The following image shows the Berstein polynomial functions of a Bézier curve of degree 5. You can see how much influence has each polynomial on the curve progression. For example at t=0 only b₀ is nonzero. Therefore all other polynomials don't have a bearing on the curve progression in the point S(t=0).

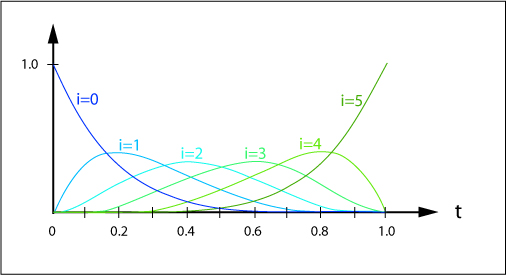
Characteristics of Bézier Curves

The following list contains the main characteristics of Bézier curves

• The starting point of the curve is P₀ and the ending point is P_n.
• Normally, the other control points are not positioned on the curve.
  
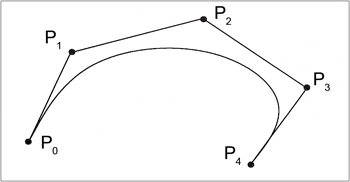  Bézier Curve of degree 4. (GIGER-HOFMANN 1992)
  
  
• The Bézier curve is completely contained in the convex hull built from the control points.
  
  
  
  
• If and only if all control points lie on the curve it is a straight line.
  
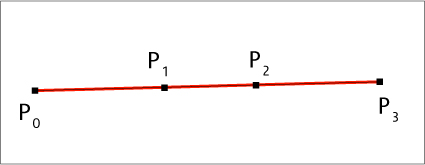  All contol points on the curve
  
  
• The start (end) of the curve is tangent to the first (last) section of the Bézier polygon.
  
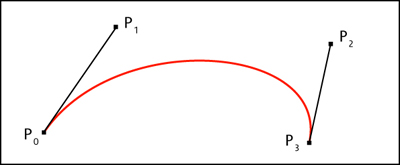  Tangents of the curve
  
  
• P_i provide the direction of the curve (they pull the curve in their direction). The weighting of the points depends on the Bernstein polynomials and therefore on t as you could see above.
  
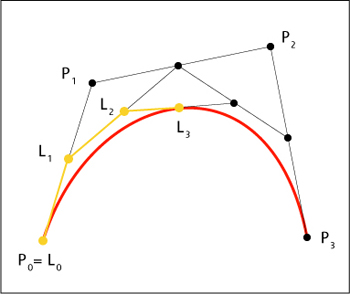
  Weighting of control points according to (WATT et al. 1998)
  
  
• A curve can be split at any point into 2 subcurves, or into arbitrarily many subcurves, each of them is also a Bézier curve.
  
  Subdivision of Bézier curves